Subjectivity in Mathematics – Implications of Richard Buckminster Fuller’s Energetic Geometry

This is an essay I have written as part of a Philosophy of Science course with Blay Whitby in Summer 2016.

Abstract

I compare Euclidean and Energetic Geometry to show how there is a set of mathematical languages, which are subjected to interpretation. This theoretical exercise provides deeper insights into the agendas and world views mathematical concepts carry and deconstruct the presumed ‘neutral’ or ‘objective’ stance that is largely attributed to them.

The Point of Euclidean Geometry

There is a large desire in human society to order the world it exist in, because “[b]eing able to see connections confirms our hope that our world is under- standable and not just a bunch of senseless accidents” [Meyer, 2006, p.5]. Consequently, around 300 BCE Euclid attempted to structure space by formally defining Elements [Euclid and Joyce, 1996].
There is just one problem. “(…) [T]here seems to be nothing in nature that is absolutely straight enough to be a “true” line segment” [Meyer, 2006, p.7]. Hence, Euclid’s geometry has to produce a symbolic system that is tightly cou- pled to rigorous rules of precision. Otherwise the geometry cannot function as an abstraction beyond a visual depiction (ibid.). This means that the underlying axioms of which formulae are deduced have to be both strict and generally applicable at the same time.
It is all the more surprising then that Euclidean geometry does not give strong definitions for its pre-axiomatic building blocks such as the point and subsequently also lines and planes [Meyer, 2006, p.22]. Rather, they remain undefined. Considering that Euclid’s geometry demands rigour and proof through axioms, it appears inconsistent that when it comes to the core parts of these axioms, Euclid relies on ’common’ knowledge of what constitutes a point. Through this, Euclid offers a subjective gateway into geometry. It becomes then situ- ated within the tools that are used to work with them (e.g., pen and paper vs. computational construction) and depends on context, that, for the sake of comparability gets abstracted away to defend the objectivity of a system, whose grammatical base has not been properly specified.
Following this, Euclidean geometry constructs meaning through the formulae and abstractions of the world, which is limited by the axiomatic space it provides. We will see how this defines discursive limits and how representations of the world contain ideological and subjective points of view.

Fuller’s Critique

During the first half of the 20th century, Richard Buckminster Fuller – alongside being a well-received architect – publicly criticised the construction of the Euclidean right angle. Fuller points out, that it relies on the opportunities and limitations provided by the instrument used. Next to the already often cited ones (ruler, compass and pen), Fuller adds another important agent into this set: the flat surface on which a right angle is constructed on [Fuller, 1999a, p.175]. This pre-axiomatic critique of Euclidean geometry can also be seen as a critical approach to the prevalent world view at the time as it shows itself by the methods and spaces spanned open by geometry as a way to measure the world.
To Fuller, mathematics as a discipline and geometry as a part of that discipline is full of ”inconsumerable ratios and a barrel full of clumsy constants” [Fuller, 1999a, p.178]. Constants such as π or e are difficult to conceive. This shows how not only the instruments, but also the creations they produce are lost in the resulting complexity. ”Whatever happens in the depths of matter, disappears behind ever larger apparatuses, which we cannot look inside and even if we could, we would not see anything and even if we saw, we wouldn’t understand it, since the quantal world doesn’t bother to shape itself in our form of sensual experience. In one word: the constructive mediatedness of our perception is in theoretical and practical aspects so overwhelming, that it becomes understandable, that some physicists don’t really know what their matter actually is.” [Mutschler, 1998, p.33, translated from German]. To Fuller, this is not acceptable. His ontology requires a world that has an image that is as easily perceivable as the world itself (Heidegger might agree, see Heidegger [1926/1967]).
Euclidean geometry and mathematical constants put a layer on the world, which does its elegance no justice [Fuller, 1999a, p.178]. Its abstractions fail to simplify the direct world, but rather construct purely nonphysical constructs such as straight lines [Fuller, 1999a, p.173]. Those who practise Euclidean geometry agree (cf. Meyer [2006, p.5]). The three dimensional space became more and more of a problem. ”The leitmotif of the 19th century, which con- nected maths, physics and philosophy, the >space problem< emerged: How can the natural space be described mathematically." [Mehrtens, 1990, p.44, translated from German]. Energetic Geometry

With the feeling ”(…) that the whole universe must be the starting point for his enquiry (…)” [Morrell, 1986, p.613], Richard Buckminster Fuller understood mathematics as a generalised form of learning which – in his opinion – should be oriented on patterns found in nature (ibid.). While I personally am not inclined to distinguish between nurture and nature, this perspectives make sense within the then contemporary major scientific paradigm.
Because Euclidean geometry is insufficient for Fuller, he developed an alter- native geometry, which he claims to be intuitive and supporting human creativity. This is especially important to him. It is interesting though, how – despite the thousands of years of the history of humankind full of innovation and archi- tecture – he claims to have developed a more fitting system that is supposed to be better for exactly what has been already achieved with an old out-dated one: the creatively built and inspiring environment in which he thinks.
To Fuller, every physical force (such as warmth, electricity and magnetism) can be described in energetic terms. A geometry delivering a more intuitive image of the world, should, hence, follow this, which is why he calls his approach Energetic Geometry. He starts with new basics, in order to follow a more strict construction of his postulates [Fuller, 1999a, p.178]. For this, he first defines his tools with the goal of an explicit mention of the inscription of tools in the the- ory they are being used by. This does neglect, that the implicit assumptions of Euclidean Geometry are not effectively circumvented, but rather made explicit.
”[T]he apparently simple and unproblematic idea of a »point« had to be rethought, and »the phenomena accommodated by the packaged word point will always prove to be a focal center of differentiating events.« For Fuller, geometry did
not describe a timeless space of pure Cartesian form, but rather a universe where lines »cannot go through the same point at the same time.«” [Nye, 2009, p.88]. Fuller tries to abstract from the undefined grounds of Euclidean geometry and defines his core elements as events and vectors connecting those. This equivalency to points and lines is being presented by Fuller himself in Fuller [1999b]. Geometrical deliberations are especially suitable for equivalent theories due to their strictly axiomatic build up. ”(…) Equivalence of axiomatic theories is given ipso facto, since every mathematical system of axioms can be described differently achieving the same. Whether something is an axiom or a theorem depends on its place in a network of mathematical relations, which can be differently arranged while accomplishing the same thing.” [Mutschler, 1998, p.29, translated from German]. Energetic geometry, hence, provides a different way of expressing the same things as Euclidean geometry.

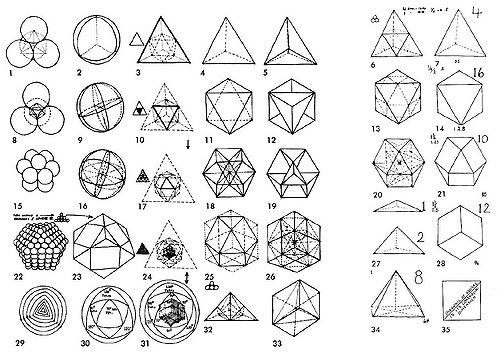
Geometry as Construct

While Fuller is by far not the first who voices issues with Euclidean geometry (see, e.g. the concept of spherical geometry Katz and Imhausen [2007, S.4]), he does provide a unique ’solution’ to the spatial problem. He does not base his work on the right angle, but rather on the rigid construct of triangular bodies and derivations thereof. Polyhedra are especially fascinating to him and also provide a way to illustrate how geometry is constructed by the language and the implicit ideologies roaming through it. Buckminster Fuller describes polyhedra as such:

(…) Every vector (line) leads from one center of a sphere to an- other and therefore represents the operational effect of melting two forces. Every vector (line) consists of two halves, each of them be- longing to one of the spheres and each half of the line represents the radius of each tangential sphere, which all are in a right angle to the identical tangent point and construct a continuous straight line: Through that it is defined that a unit (represented by the inter nuclear vector-module) necessarily holds double the value, which means: unity is inherently two, since it represents the unity of at least two centers of energy. [Fuller, 1999b, S.183, translated from German]

In comparison, the definition of a polyhedron from a Euclidean perspective:

A polyhedron is a three-dimensional solid bounded by a finite number of polygons called faces. Points where three or more faces meet are called vertices. Line segments where exactly two faces meet at an angle are called edges. The vertices and edges of a polyhedron make a graph called the graph of the polyhedron. [Meyer, 2006, S.418]

It should be mentioned, thought, that rigid polyhedra are rare to find and often constructed by humans. “There were only a few polyhedra to be found in nature or the man-made world at that time in history: rooms of buildings, which are basically rectangular parallelopipeds; the pyramids of Egypt; and perhaps a few other examples.” [Meyer, 2006, S.432]. Therefore, polyhedra are more of a thought experiment in other versions of geometry.
Interestingly enough, although Fuller attacks the straight line with a passion only two years earlier [Fuller, 1999a], he now re-establishes it. He also just renames points and calls them centres of spheres. Hence, it is not necessarily the mathematical consistency, he attacks in Euclidean geometry. His agenda is a different one.
The difference between the two definitions can be seen especially in the lines (or vectors). Fuller’s centres of energy are loaded with meaning while Euclidean geometry tries desperately to keep all meaning out, which necessarily fails. The basis from which we construct, analyse and depict the world around us, is, hence constructed in and off itself only providing another tool to express what we perceive.
Another example for a different dialect within geometry is Hilbert’s. ”(…) [Y]ou can extract the graphic model of Euclidean geometry from the abstraction of Hilbert geometry.” [Mutschler, 1998, p.35, translated from German]. Since one geometrical system can be translated in another, we can understand it as a language system. In that context, we can see mathematics as one language and different versions of it as dialects.
However, then geometry cannot be what it claims it is: an accurate depiction of the perceivable world. ”If it depends on the phrasing of a theory on whether a space is Euclidean or not, whether reality consists of particles or fields, then we cannot naively understand the theoretical concepts as portrayal of a world being for itself.” [Mutschler, 1998, S. 35, translated from German]. Fuller’s energetic geometry, hence, shows how mathematical systems are subject to interpretation and are con- structed through their perception every time. The societal agreement on how to ’properly’ construct the meaning given by Euclidean geometry is fairly rigorous in the western world; that doesn’t necessitate only one way to understand it, though.

References

Euclid and David E Joyce. Euclid’s Elements. Clark University, Department of Mathematics and Computer Science, 1996.

Richard Buckminster Fuller. Dymaxion Comprehensive System – Einführung Energetischer Geometrie (1944). In Richard Buckminster Fuller, Joachim Krausse, and Claude Lichtenstein, editors, Your Private Sky: R. Buckminster Fuller: The Art of Design Science, pages 172–181. Springer, 1999a.

Richard Buckminster Fuller. Energetische Geometrie (1946) /Dichteste Packung von Kugeln). In Richard Buckminster Fuller, Joachim Krausse, and Claude Lichtenstein, editors, Your Private Sky: R. Buckminster Fuller: The Art of Design Science, pages 182–183. Springer, 1999b.

Martin Heidegger. Sein und Zeit. Max Niemeyer Verlag Tübingen, 1926/1967.

Victor J Katz and Annette Imhausen. The Mathematics of Egypt, Mesopotamia, China, India and Islam: A Source Book. Princeton University Press, 2007.

Herbert Mehrtens. Moderne – Sprache – Mathematik: Eine Geschichte des Streits um die Grundlagen der Disziplin und des Subjekts formaler Systeme. Suhrkamp, Frankfurt, 1990.

Walter A Meyer. Geometry and its Applications. Access Online via Elsevier, 2006.

William R. Morrell. Some Perspectives of Fuller’s Mathematics – An Undergraduate’s Assessment by William R. Morrell, Yale College, Class of 1986. In Robert W. Gray, editor, Synergetics Dictionary Online, pages 613–618. Online: http://www.rwgrayprojects.com/ SynergeticsDictionary/status.html, 1986.

Hans-Dieter Mutschler. Die Welt als Konstruktion. In Kurt Komarek and Gottfried Magerl, editors, Virtualität und Realität. Bild und Wirklichkeit in den Naturwissenschaften, pages 25–42. Wien; Köln; Weimar : Böhlau, 1998.

David E. Nye. Energy in the Thought and Design of R. Buckminster Fuller. In Hsiao-yun Chu and Roberto G Trujillo, editors, New Views on R. Buckminster Fuller, pages 86–98. Stanford University Press, 2009.